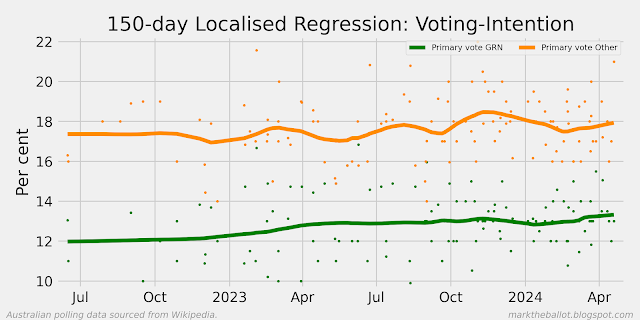
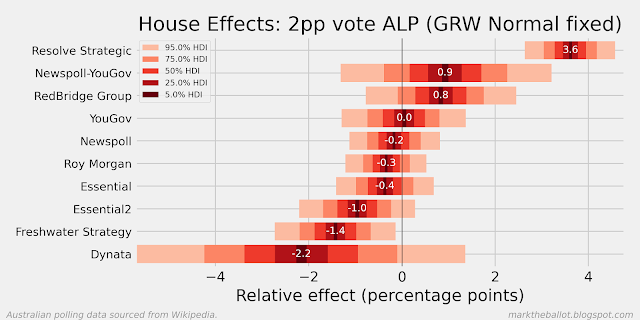
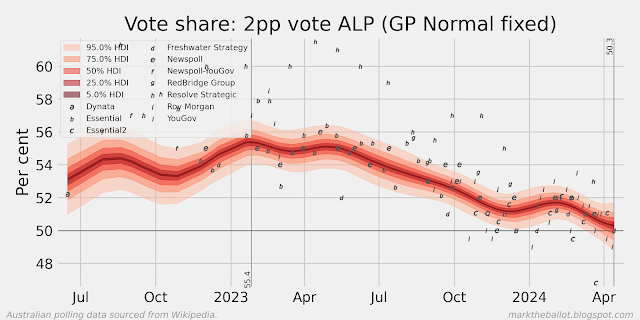
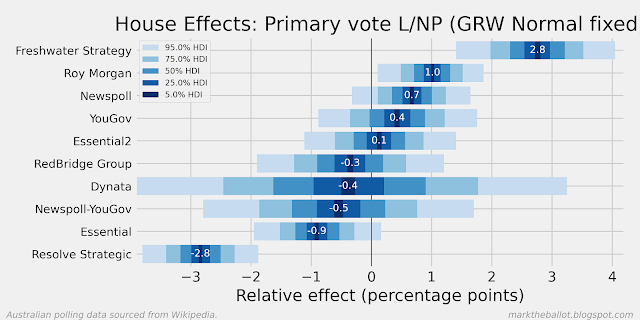
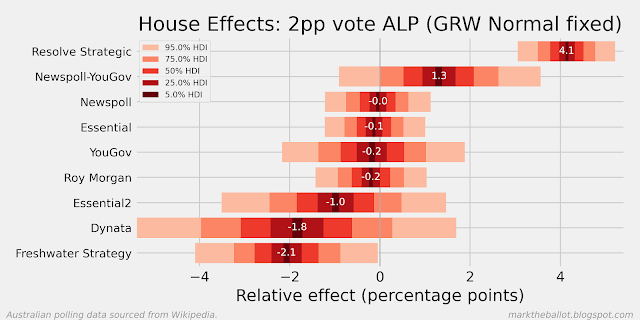
When I look at the recent polls from Resolve Strategic, it looks like the polls from 2024 are less favourable to Labour than the polls from the prior two years. In the first chart below, we can see that the last poll result was almost four percentage points more favourable to the Coalition than the long term average for Resolve Strategic. In the second chart below, we can see that historically Resolve Strategic has been the most favourable poll for Labor (on average). And in the third chart below, we can see that the individual Resolve Strategic polls in 2022 and 2023 (indicated with the letter h) were often (but not always) well above the aggregation, and two of the three polls in 2024 are not.
Now, this could be just the usual random noise and chance that comes with statistics. And in coming months we will see a return of the prior patterns of systemic house bias at Resolve Strategic. But this apparent change could also be the result of a change in polling methodology at Resolve Strategic. At the moment I don't know which explanation is the most plausible. While I have looked, I have not seen a statement on any methodology change from Resolve Strategic (please provide a link below in the comments if I have simply missed it).
If this apparent change in house bias is sustained in the next couple of Resolve Strategic polls, I will assume that there has been something of a change in polling methodology, and I will separate the 2024 and subsequent polls into their own series.
Please note: this is not a criticism of Resolve Strategic. I have enormous respect for all pollsters, and I appreciate that opinion polling is much harder today than it was (say) 35 years ago (when almost every house had a landline and no-one had mobile phones). At the moment, I am just observing that the last three polls from Resolve Strategic perhaps look a little different from the earlier polls, and I am musing why this might be the case. Nonetheless, I would be somewhat disappointed if it turns out that Resolve Strategic has changed its polling methodology but has not communicated how it has changed and why it has changed.